Table of Contents
Shortest Path Problem
Use the solver in Excel to find the shortest path from node S to node T in an undirected network. Points in a network are called nodes (S A B C D E and T). Lines in a network are called arcs (SA SB SC AC etc).
Formulate the Model
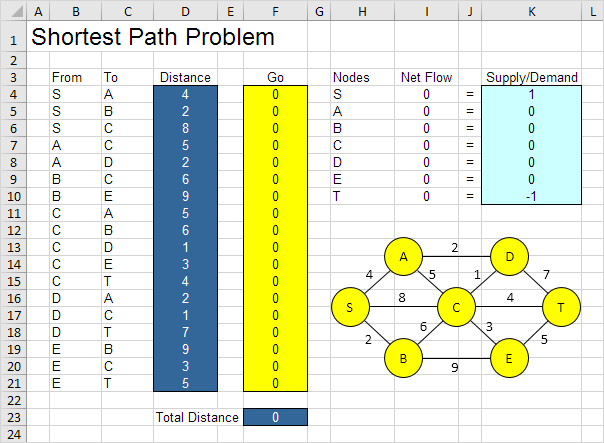
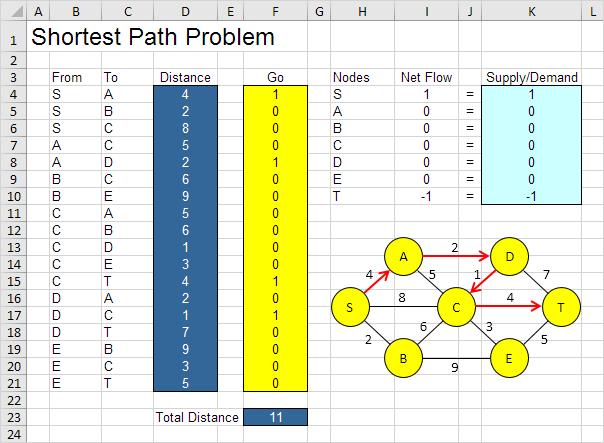
The model we are going to solve looks as follows in Excel.
1. To formulate this shortest path problem answer the following three questions.
a. What are the decisions to be made? For this problem we need Excel to find out if an arc is on the shortest path or not (Yes=1 No=0). For example if SB is part of the shortest path cell F5 equals 1. If not cell F5 equals 0.
b. What are the constraints on these decisions? The Net Flow (Flow Out – Flow In) of each node should be equal to Supply/Demand. Node S should only have one outgoing arc (Net Flow = 1). Node T should only have one ingoing arc (Net Flow = -1). All other nodes should have one outgoing arc and one ingoing arc if the node is on the shortest path (Net Flow = 0) or no flow (Net Flow = 0).
c. What is the overall measure of performance for these decisions? The overall measure of performance is the total distance of the shortest path so the objective is to minimize this quantity.
2. To make the model easier to understand create the following named ranges.
| Range Name | Cells |
|---|---|
| From | B4:B21 |
| To | C4:C21 |
| Distance | D4:D21 |
| Go | F4:F21 |
| NetFlow | I4:I10 |
| SupplyDemand | K4:K10 |
| TotalDistance | F23 |
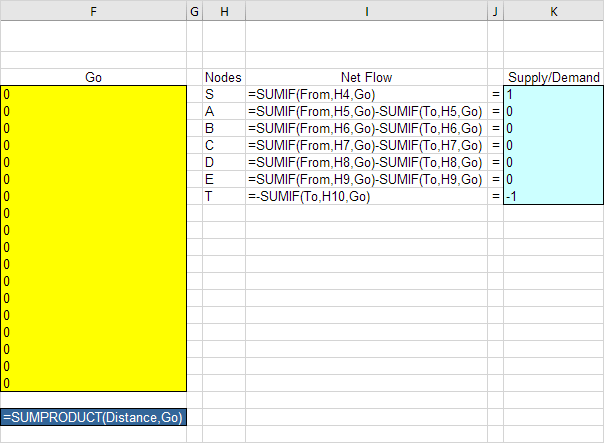
3. Insert the following functions.
Explanation: The SUMIF functions calculate the Net Flow of each node. For node S the SUMIF function sums the values in the Go column with an “S” in the From column. As a result only cell F4 F5 or F6 can be 1 (one outgoing arc). For node T the SUMIF function sums the values in the Go column with a “T” in the To column. As a result only cell F15 F18 or F21 can be 1 (one ingoing arc). For all other nodes Excel looks in the From and To column. Total Distance equals the sumproduct of Distance and Go.
Trial and Error
With this formulation it becomes easy to analyze any trial solution.
1. For example the path SBET has a total distance of 16.
It is not necessary to use trial and error. We shall describe next how the Excel Solver can be used to quickly find the optimal solution.
Solve the Model
To find the optimal solution execute the following steps.
1. On the Data tab in the Analyze group click Solver.
Note: can’t find the Solver button? Click here to load the Solver add-in.
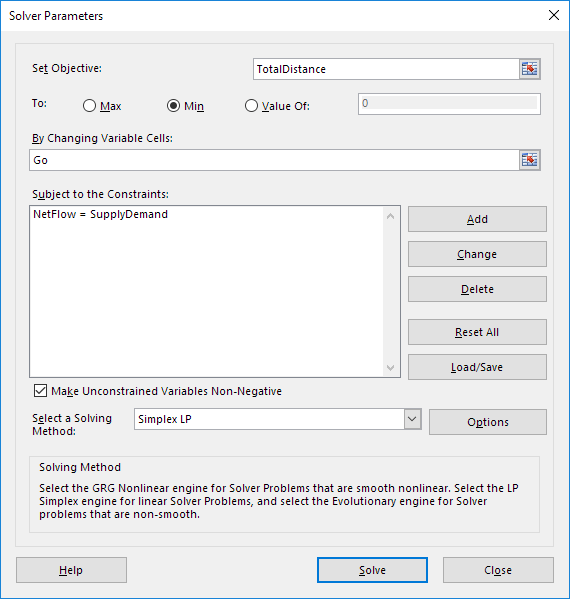
Enter the solver parameters (read on). The result should be consistent with the picture below.
You have the choice of typing the range names or clicking on the cells in the spreadsheet.
2. Enter TotalDistance for the Objective.
3. Click Min.
4. Enter Go for the Changing Variable Cells.
5. Click Add to enter the following constraint.
6. Check ‘Make Unconstrained Variables Non-Negative’ and select ‘Simplex LP’.
7. Finally click Solve.
Result:
The optimal solution:
Conclusion: SADCT is the shortest path with a total distance of 11.